Быть учителем - самая благородная миссия на Земле: учитель своими руками творит характер, индивидуальность,личность ребенка, творит его Будущее и, в конечном счете, - Будущее планеты.






Звёздчатый многогранник (звёздчатое тело) - это невыпуклый многогранник, грани которого пересекаются между собой.
Звёздчатой формой многогранника называется многогранник, полученный путем продления граней данного многогранника через ребра до их следующего пересечения с другими гранями по новым рёбрам.
Правильные звёздчатые многогранники — это звёздчатые многогранники, гранями которых являются одинаковые правильные или звёздчатые многоугольники. Коши установил, что существует всего 4 правильных звёздчатых тела, не являющиеся соединениями платоновых и звёздчатых тел, называемые телами Кепплера — Пуансо: все 3 звёздчатых формы додекаэдра и одна из звёздчатых форм икосаэдра.Остальные правильные звёздчатые многогранники являются или соединениями платоновых тел, или соединениями тел Кепплера — Пуансо.


Малый звездчатый додекаэдр
Большой додекаэдр
Большой звездчатый додекаэдр
Большой икосаэдр



Правильные многогранники с древних времен привлекали внимание философов, строителей, архитекторов, художников, математиков. Их поражала красота, совершенство, гармония этих фигур.
Правильный многогранник – объёмная выпуклая геометрическая фигура, все грани которой - одинаковые правильные многоугольники и все многогранные углы при вершинах равны между собой. Существует множество правильных многоугольников, но правильных многогранников всего пять. Названия этих многогранников пришли из Древней Греции, и в них указывается число («тетра» - 4, «гекса» - 6, «окта» - 8, «додека» - 12, «икоса» - 20) граней («эдра»). Пять платоновых тел были гордостью Пифагорейской школы.
Тетраэдр
Октаэдр
Гексаэдр (куб)
Икосаэдр
Додекаэдр
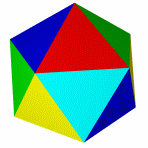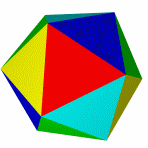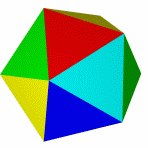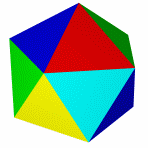



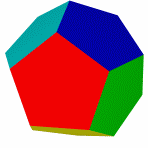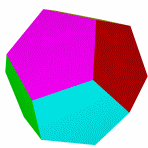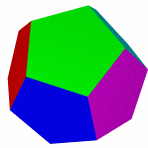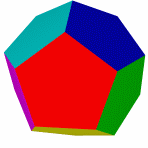
Тетраэдр и гексаэдр (куб) не имеют звёздчатых форм, так как их грани при продлении через рёбра более непересекаются.
Звёздчатый октаэдр
Звёздчатые формы додекаэдра
Додекаэдр имеет 3 звёздчатые формы: малый звёздчатый додекаэдр, большойдодекаэдр, большой звёздчатый додекаэдр (звёздчатый большой додекаэдр, завершающая форма). Первые две из них были открыты Кеплером (1619), третья — Пуансо (1809). В отличие от октаэдра любая из звёздчатых форм додекаэдра не является соединением платоновых тел, а образует новый многогранник.
Все 3 звёздчатые формы додекаэдра, вместе с большим икосаэдром образуют семейство тел Кеплера-Пуансо, то есть правильных невыпуклых (звёздчатых) многогранников.
У большого додекаэдра гранями являются пятиугольники, которые, сходятся по пять в каждой из вершин. У малого звёздчатого и большого звёздчатого додекаэдров грани - пятиконечные звёзды (пентаграммы), которые в первом случае сходятся по 5, а во втором по 3.
Вершины большого звёздчатого додекаэдра совпадают с вершинами описанного додекаэдра. У каждойвершины соединяются три грани.
Звёздчатые формы икосаэдра
Икосаэдр имеет 59 звёздчатых форм, из которых 32 обладают полной, а 27 неполной икосаэдральной симметрией, что было доказано Кокстером совместно с Дювалем, Флэзером и Петри c применением правил ограничения, установленных Дж. Миллером. Одна из этих звёздчатых форм (20-я, мод. 41 по Веннинджеру), называемая большим икосаэдром, является одним из четырёх правильных звёздчатых многогранников Кеплера—Пуансо. Его гранями являются правильные треугольники, которые сходятся в каждой вершине по пять; это свойство является у большого икосаэдра общим с икосаэдром.
Икосаэдр имеет двадцать граней. Если каждую из них продолжить неограниченно, то тело будет окружено большим многообразием отсеков — частей пространства, ограниченных плоскостями граней. Все звёздчатые формы икосаэдра можно получить добавлением к исходному телу таких отсеков. Не считая самого икосаэдра, продолжения его граней отделяют от пространства 20+30+60+20+60+120+12+30+60+60 отсеков десяти различных форм и размеров. Большой икосаэдр состоит из всех этих кусков, за исключением последних шестидесяти.
"Вторая" звездчатая
форма икосаэдра

Звёздчатые формы кубооктаэдра
Кубооктаэдр – полуправильный многогранник. Он строится так: в кубе проводятся отсекающие плоскости через середину ребер, выходящих из одной вершины. В результате получится полуправильный многогранник - кубооктаэдр. Его гранями являются шесть квадратов, как у куба, и восемь правильных треугольников, как у октаэдра. Отсюда и его название.
Кубооктаэдр имеет 4 звёздчатые формы, удовлетворяющие ограничениям, введённым Миллером. Первая из них является соединением куба и октаэдра.
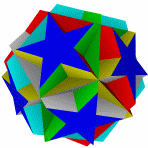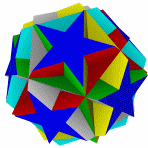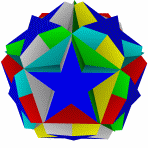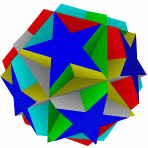
Звёздчатые формы икосододекаэдра
Соединение куба и октаэдра

Кубооктаэдр

Завершающая звездчатая форма кубоктаэдра

Звездоформа кубоктаэдра

Звездчатые формы икосаэдра


Икосододекаэдр

Икосододекаэдр имеет 32 грани, из которых 12 являются правильными пятиугольными гранями, а остальные 20 — правильные треугольники. Что касается вопроса о том, могут ли получившиеся многогранники оказаться правильными, то на него давно получен ответ. Великий математик Коши ещё в 1811 году доказал, что список правильных многогранников исчерпывается пятью платоновыми телами вкупе с четырьмя многогранниками Кеплера — Пуансо.
Икосододекаэдр имеет множество звёздчатых форм.
Соединение икосаэдра
и додекаэдра

Завершающая звездчатая
форма икосододекаэдра

Звездоформы икосододекаэдра



Превалирует большой Но он становится все и меньше и меньше и исчезает совсем
звездчатый додекаэдр меньше





Соединение пяти тетраэдров

Соединение десяти тетраэдров

Усеченный тет�раэдр Усеченный октаэдр Усеченный куб Усеченный икосаэдр Усеченный додекаэдр

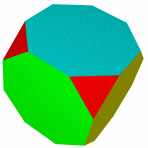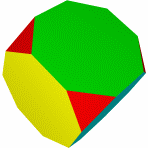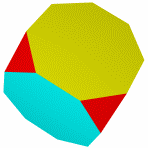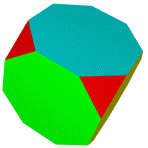
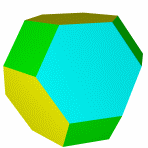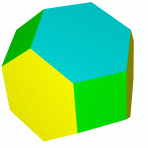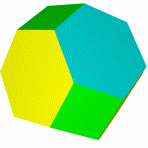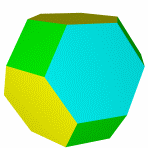
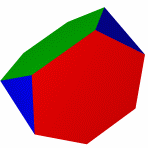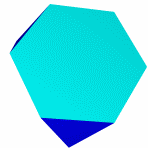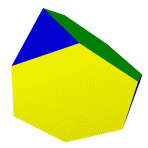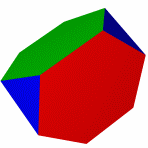

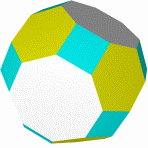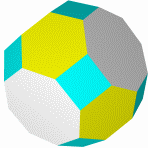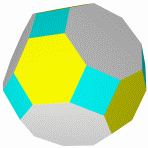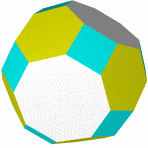
Кубооктаэдр Икосододекаэдр Ромбокубоктаэдр Ромбоикосододекаэдр




Ромбоусеченный Ромбоусеченный Курносый куб Курносый додекаэдр
кубооктаэдр икосододекаэдр

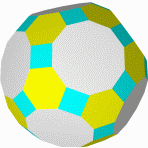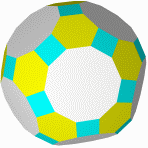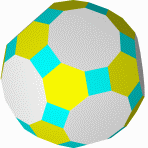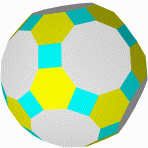

Тетрагемигексаэдр Октагемиоктаэдр Кубогемиоктаэдр Малый Малый
икосогемидодекаэдр додекогемидодекаэдр


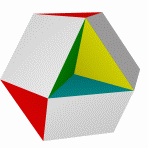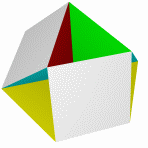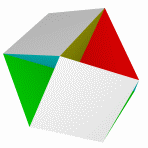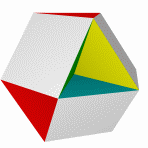

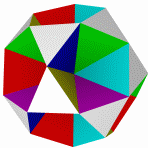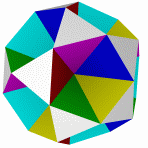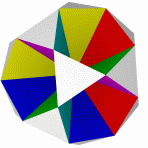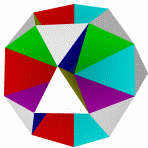
Большой кубокубооктаэдр Большой ромбогексаэдр Малый кубокубоктаэдр Малый ромбогексаэдр Квазиромбокубоктаэдр




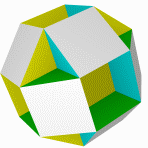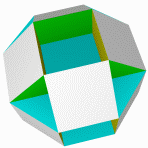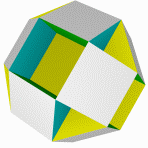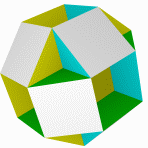
Малый додекоикосододекаэдр Малый ромбододекаэдр Усеченный большой Додекододекаэдр Малый додекогемиикосаэдр додекаэдр
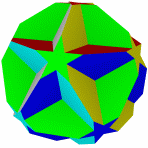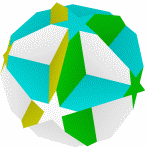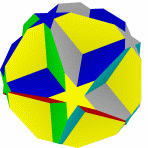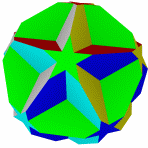
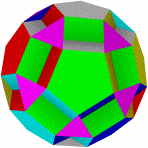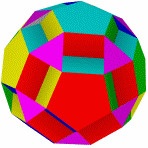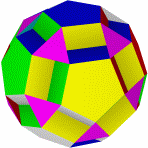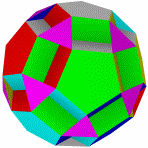



Большой Усеченный большой Малый битригональный Битригональный додекаэдр Большой битригональный
додекогемиикосаэдр икосаэдр икосододекаэдр икосододекаэдр


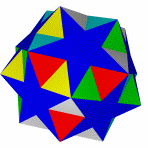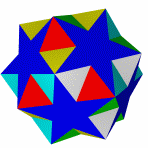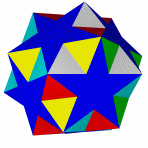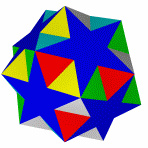

Существует только одна звёздчатая форма октаэдра. Звёздчатый октаэдр был открыт Леонардо да Винчи, затем спустя почти 100 лет переоткрыт Иоганном Кеплером, и назван им Stella octangula — звезда восьмиугольная. Отсюда эта форма имеет и второе название stella octangula Кеплера. По сути она является соединением двух тетраэдров.

Работы моих учеников, 6 класс



Малый икосоикосододекаэдр Малый битригональный Малый додекоикосаэдр Ромбододекододекаэдр Икосододекододекаэдр
додекоикосододекаэдр
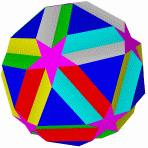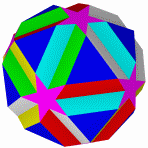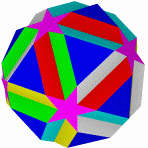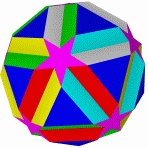



Ромбоикосаэдр Кубоусеченный кубооктаэдр Икосододекоусеченный Квазиусеченный Квазиусеченный додекаэдр
икосододекаэдр кубооктаэдр



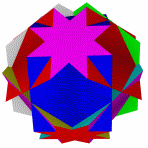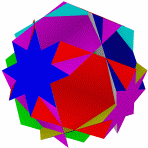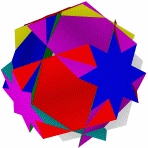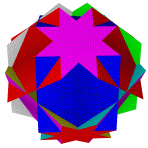

Большой битригональный Большой додекоикосаэдр Большой Квазиусеченный гексаэдр Большой икосододекаэдр
додекоикосододекаэдр икосоикосододекаэдр


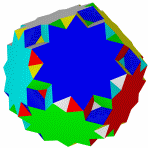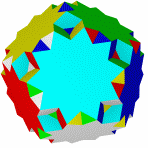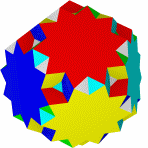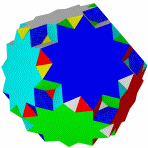

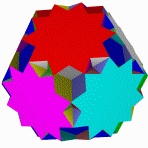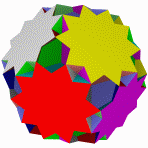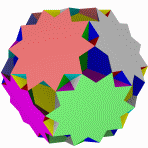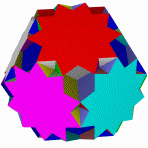
Большой икосогемидодекаэдр Большой Квазиусеченный звездчатый Квазиусеченный большой Большой
додекогемидодекаэдр додекаэдр звездчатый додекаэдр додекоикосододекаэдр



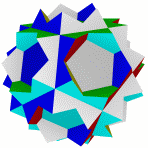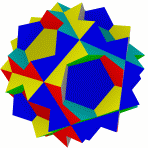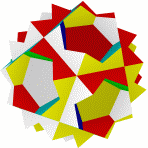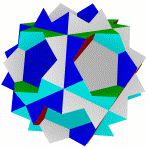
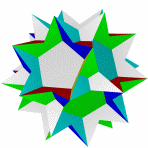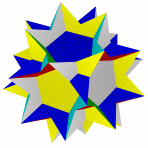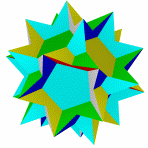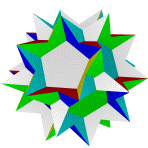
Квазиромбоикосододекаэдр Большой ромбододекаэдр Большой квазиусеченный Малый курносый Курносый додекододекаэдр икосододекаэдр икосододекаэдр





Курносый Большой вывернутый курносый Вывернутый курносый Большой курносый Большой курносый
икосододекододекаэдр икосододекаэдр додекододекаэдр додекоикосододекаэдр икосододекаэдр






Большой вывернутый Малый вывернутый обратнокурносый Большой биромбоикосододекаэдр
обратнокурносый икосододекаэдр икосоикосододекаэдр


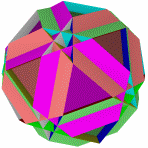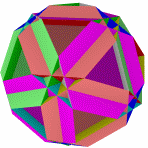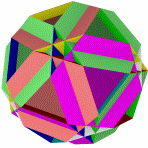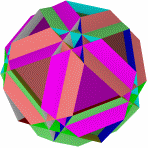
Завершающая звездчатая форма ромбоикосододекаэдра. Появление ромбической грани привело к резкому увеличению изрезанности пиков

Одна из звездчатых форм курносого додекаэдра. Просто поражает своею сложностью!

Псевдо вариант квазиусеченного кубоктаэдра. Эта тело не упоминается в книге Веннинджера "Модели многогранников", хотя и много пишут о псевдоварианте квазикубоктаэдра.

